Cost Function
비용함수를 사용해서 주어진 데이터에 가장 가까운 1차함수 그래프를 알아낼 수 있다.
01 에서 봤던 예시를 다시 가져오자.
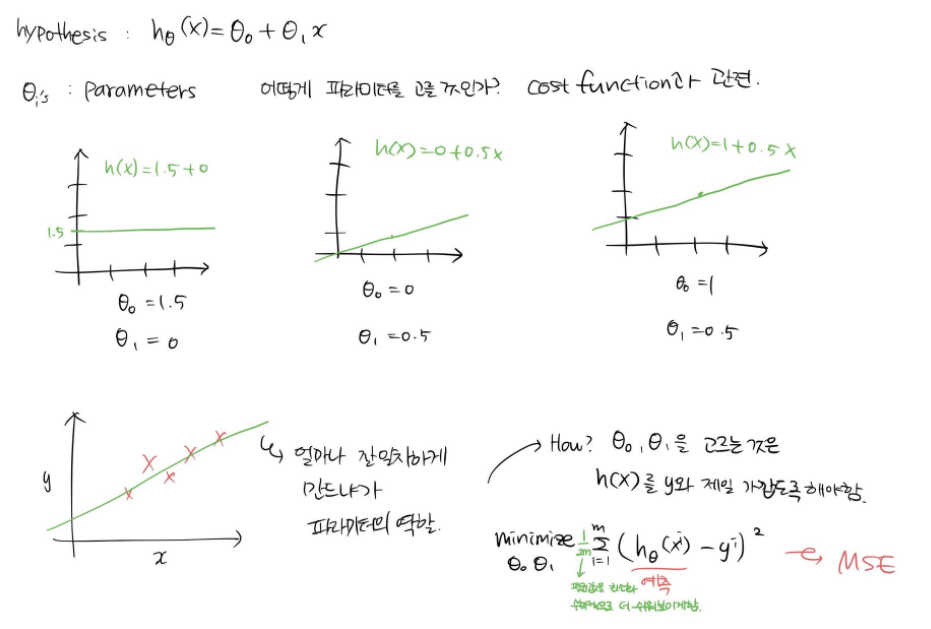
"𝜃_0과 𝜃_1을 어떻게 고를 것이냐" 를 위해 비용함수를 사용한다. 각 파라미터의 값에 따라 추세선이 달라진다.
우리가 𝜃_0과 𝜃_1을 선택했을 때 이것이 데이터와 얼마나 잘 일치하는지 어떻게 알 수 있을까?
h(x)와 y간의 차를 작게 하면된다.
Mean Square Error

평균값을 최소화하기 위해서 1/2m을 곱한다.
우리는 위 함수를 예제문제의 비용함수로 사용할 수 있다.
MSE는 주로 회귀 문제에서 잘 작동한다. 이 외의 많은 오차함수들이 있다.
정리해보면,

h(x)와 J(𝜃)를 잘 구분해야한다.
h(x)는 가설이며 x의 함수이다. 𝜃는 고정되어 있고, x의 값 변화에 따라 그래프가 그려진다.
J(𝜃)는 비용함수이며 𝜃에 대한 함수이다. 𝜃의 값에 따라 그래프가 달라진다.

우리는 비용함수 J(𝜃)를 최소화 시키는 것이 목적이다.
왜냐하면 비용함수 J(𝜃)가 최소화되어야 데이터와 예측 간의 차이가 적다는 것이기 때문이다.
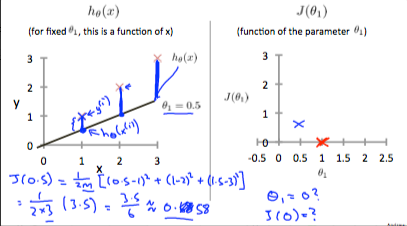
𝜃값을 변화시키면서 비용함수J(𝜃)를 구해보면 아래와 같은 그래프가 그려진다.
우리는 이러한 그래프에 미분을 하여 경사를 하강하게 된다. (gradient descent)
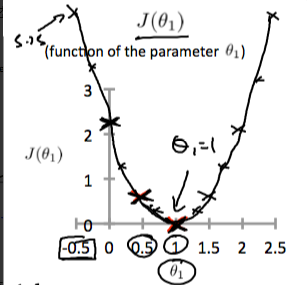
좀 더 직관적으로 cost function을 이해해보자.

1개의 파라미터만 따졌을 때는 2차 함수의 모양이 나왔다. 그러나 2개 이상의 파라미터를 최소화하기 위한 cost function의 그래프는 3차원 이상이 된다.

이런 형태를 매번 쓸 수 없으니 등고선 형태(contour graph)를 사용할 것이다.

우리는 이러한 그래프를 보고 일일이 값을 읽으면서 문제를 풀고 싶은 것이 아니다.
그래서 사용하는 것이 Gradient Descent 이다.
'Machine Learning' 카테고리의 다른 글
| 코세라 - 04 Multiple features (0) | 2019.08.30 |
|---|---|
| 코세라 - 03 Gradient Descent (0) | 2019.08.30 |
| 코세라 - 01 Model Representation (0) | 2019.08.30 |
| 코세라 - 00 Machine Learning (0) | 2019.08.30 |
| (edwith) 인공지능 및 기계학습 개론 (2) MLE - 문일철 교수님 (0) | 2019.05.02 |