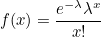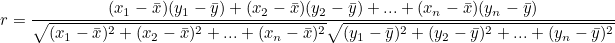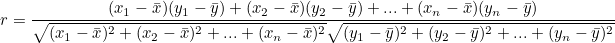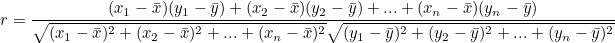양갱로그

> F분포 F값은 2개의 x의 제곱값의 비로 정의된다. 이 비의 분포를 F 분포라고 한다. 두 개의 X제곱값을 사용하기 때문에 자유도는 2개가 된다. m1은 분자의 자유도, m2는 분모의 자유도이고 아래와 같이 표현한다. > t분포 모분산을 알 수 없고, 표본의 크기가 작을 때 z분포(정규분포)를 사용하여 검정하면 결과가 틀릴 수 있다. 이런 경우, 스튜던트화 변량이 따르는 t분포를 사용한다. t분포는 자유도에 따라 분포 형태가 달라진다. t(자유도) 로 표현한다. 모분산을 모르는 것은 모표준편차도 알 수 없다는 것이다. 이럴 때 정규분포 대신 사용하는데 식은 다음과 같다. S는 원래 모표준편차 값이 되어야하는데, 값을 모르기 때문에 t분포의 표본표준편차(s)를 사용한다. 표본 크기가 커질수록 정규분포와..

> 포아송 분포 시행 횟수가 아주 많고, 사상 발생 확률이 아주 작을 때의 이항분포 공장에서 물건을 생산할 때 불량품의 수와 같이 시행 횟수는 많으나 적게 발생하는 사항의 확률 분포를 나타내는데 이용한다. e = 네이피어 상수, λ = 평균값(시행횟수 * 확률), x = 사상이 일어나는 횟수 평균값이 왜 시행횟수 * 확률일까는 이 블로그를 참고하자 이항분포의 기댓값은 시행횟수 * 확률이다. 포아송 분포의 람다값이 커지면, 즉 n 또는 p 값이 커지면 분산이 커지고, 분포곡선이 오른쪽으로 이동한다. 결과적으로는 정규분포에 가까워진다. > 카이제곱 분포 카이제곱 분포는 정규분포를 따르는 여러 데이터를 한 번에 취급하는 것이 가능하다. 이 때문에 분산분석에 이용할 수 있고 제곱하면 자유도에 따라 분포 형태가 ..

정규분포는 평균값을 중심으로 대칭을 이루는 종 모양의 분포 통계학에서 가장 중요한 분포라고 할 수 있다. 이항분포의 시행 횟수를 늘리면 분포가 정규분포에 가까워진다. > 표준정규분포 (standard normal distribution, z-distribution) 표준정규분포란 말그대로 표준화한 정규분포를 말한다. 표준화라는 것은 무엇일까? 표준화는 평균값을 0, 분산 1로 변환하는 것을 말한다. 표준화변량 식은 다음과 같다. μ는 평균, σ는 표준편차다. 편차는 데이터 값과 평균 값의 차이이다. 표준화하면 데이터가 표준정규분포의 어디에 위치하는지 알 수 있다. z의 값이 3σ 구간(99.7%) 밖에 있을 때, 잘 발생하지 않는 수이다. > 왜도 분포가 좌우대칭인지, 왼쪽 또는 오른쪽으로 치우쳐져있는지..

확률 공부를 할 때, 처음 접하는 예제는 주로 "동전 던지기" 일 것이다. 동전 던지기는 동전의 면이 '앞' 또는 '뒤'라는 사상을 가지고 있다. 이렇게 2가지 종류의 결과만 있는 시행을 베르누이 시행이라고 하고 배르누이 시행의 사상에 대한 분포를 베르누이 분포, 이항분포라고 한다. ex) 동전 던지기의 앞면 - 성공(x=1), 뒷면 - 실패(x=0)라고 표기 1회 시행으로 성공할 확률 P(x=1) = 1/2 = 0.5 1회 시행으로 실패할 확률 P(x=0) = 1-P(x=1) = 1-0.5 = 0.5 1회에 성공하고 2, 3회에 실패할 확률 P(x=1, x=0, x=0), P(x=1)*P(x=0)*P(x=0)=0.5*0.5*0.5 = 0.125 3회 시행으로 1회 성공하고 2회 실패할 확률 3회 시행으..

지난 번 용어 정리때 사상은 시행에 일어난 결과를 말한다고 했다. 균등분포 (=균일분포)는 각 사상이 일어나는 확률이 같은 분포이다. 균등분포는 이산형과 연속형 둘 다 있다. > 이산균등분포 주사위 눈을 던져서 각 눈이 나올 확률과 같이 나올 확률이 이산적인 값을 취하고 모든 결과가 나올 확률이 같은 경우, 균일분포를 따른다고 말한다. > 연속균등분포 연속균일분포는 확률변수가 연속적인 값을 취할 수 있고, 모두 같은 확률로 사상이 일어날 때 연속균등분포를 따른다고 할 수 있다. ex)

이제 확률에 대해 본격적으로 정리한다. 용어 정리가 잘 되어있지 않으면 나중에 구간추정 등에서 헷갈리는 문제가 생긴다. > 사상 (mapping) 실험과 같은 행위를 시행이라고 하는데, 이 시행에 의해 생긴 결과를 사상이라고 한다. 주사위 던지기 시행을 하면 '나온 눈'이 사상에 해당된다. > 확률 (probability) 어떤 사상이 어느 정도로 일어나기 쉬운지를 수치화한 것이다. 모든 사상에 대한 확률의 합은 1이다. 1 = 100% > 확률변수 (random variable) 시행했을 때 결과를 알 수 있는 변수를 확률 변수라고 한다. 확률 변수가 가질 수 있는 값이 1, 2, 3 이런식으로 값의 수가 유한한 것을 이산확률변수라고 한다. 만약 무한하게 연속적으로 가질 수 있는 값, 몸무게나 키 등이..