평균 값만으로는 데이터가 어떻게 흩어져 있는지 알 수 없다.
따라서 최댓값(max), 최솟값(min), 분위수(Quantile), 사분위범위(interquartile range, IQR), 분산(Variance) 등을 사용하여 데이터의 흩어진 정도를 파악한다.
> 분위수(Quantile)
n개의 데이터를 오름차순(작은 수부터 큰 수 순)으로 늘어놓고, 그것을 k등분하여 그 경계가 된 수치를 분위수라고 한다.
k=4인 사분위수가 가장 많이 사용된다.
제2사분위수는 전체 데이터의 중앙에 위치하기 때문에 중앙값(median)이라고도 한다.
ex) X = {2,2,5,3,4,7,6,1,5,3,8,9}
정렬한 X = {1, 2, 2, 3, 3, 4, 5, 5, 6, 7, 8, 9}
k=4, [1, 2, 2] | [3, 3, 4] | [5, 5, 6] | [7, 8, 9] 각 분위수 양쪽 값의 산술 평균 값이 분위수 값이 된다.
> 사분위 범위
제 3사분위수와 제 1사분위수의 차
데이터가 중앙값에 집중되어있을수록 사분위 범위가 작아진다.
> 편차(Deviation)
데이터의 값과 평균값의 차
편차가 큰 데이터가 많으면 분산이 크다고 말할 수 있다.
편차 = 관측값 - 평균값
> 분산(Variance)
데이터 전체에 대해 평균값과 차를 구해 제곱하여 더한 값에 데이터 수 n으로 나눈 값이다.
편차는 각 개별 데이터마다 계산한다는 차이가 있다.
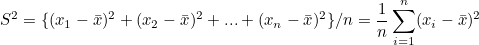
분산의 양의 제곱근을 표준편차라고 한다.
> 이상치(Outlier)
데이터의 평균에서 멀리 떨어진 값
> 변동계수
두 개의 데이터가 흩어진 정도를 비교하는 경우에 사용
더 쉽게 말하면, 두 항목이 있을 때 데이터 변동의 폭이 큰 쪽이 어디인지 비교할 때 사용한다.
변동계수는 표준편차를 산술평균으로 나눈 값이다.

'Machine Learning > Statistics' 카테고리의 다른 글
| 통계학 도감 정리 - 확률분포 1. 확률과 확률분포 (0) | 2022.03.15 |
|---|---|
| 통계학 도감 정리 - 기술통계학 3. 상관계수 (0) | 2022.03.15 |
| 통계학 도감 정리 - 기술 통계학 1. 평균 (0) | 2022.03.14 |
| 통계학 도감 정리 - 통계학이란? (0) | 2022.03.14 |
| 여러가지 확률분포 (0) | 2022.02.03 |