edwith에서 제공하는 인공지능 및 기계학습 개론 - 문일철 | KOOC (KAIST Open Online Course) 를 수강하며 정리한 글입니다.
Thumbtack Question
동전 던지기처럼 압정을 던져 압정이 떨어진 모양을 이용한 게임이 있다.
압정이 떨어진 모양에 대한 확률을 어떻게 구할 수 있을까?
일단은 몇 번 던져볼 것이다.
총 5번을 던져서 나온 결과
3/5 to nail's up case
2/5 to nail's down case
이 trial로 "up이 더 많이 나왔으니 up일 확률이 높아요."라고 하기엔 부족함이 있다.
Binomial Distribution
Binomial Distribution은 Discrete probability distribution이다.
즉, 이산확률분포이다.
ex) 동전을 던지면 1(앞), 0(뒤)가 나오게 되며 0.73 이런 식으로 결과가 나오지 않는다.
동전 던지기처럼 결과 개수가 유한하며 셀 수 있는 경우를 Discrete하다고 하고
실수값으로 표현되듯이 연속된 값을 continuous하다고 한다.
Flips are i.i.d
i.i.d = Independent and Identically distributed
랜덤확률변수들의 집합이 있을 때, 각각의 랜덤확률변수들은 독립이면서 동일한 분포를 따르는 것을 말한다.
압정 게임으로 생각해보면,
압정은 한 번 던지고 두 번 던질 때, 두 번째 던진 압정은 처음 시도된 압정게임의 영향을 받지 않는다.
즉, 각 사건이 독립이라는 것이다.
그리고 압정은 던질 때 마다 같은 분포를 따르고 있다.
P(H) = θ, P(T) = 1-θ : Head가 나올 확률이 θ이면 Tail이 나올 확률은 1-θ이다.

로 나타낼 수 있다.
우리가 가진 Data를 D라고 하고 이것은 (H,H,T,H,T)이다.
n = 5 // 던진 횟수
k = a_H = 3 //head 뽑은 수
p = θ // 압정이 주는 확률

로 계산할 수 있다.
n과 p를 안다면, K가 k일 확률을 구할 수 있다.


MLE (Maximum Likeligood Estimation)
likelihood : 가능도, 우도라고 한다. 어떤 확률변수가 그 상태를 가질 가능도이다.
우리는 우리가 가진 Data D가 만들어질 P를 정의할 수 있었다.

MLE는 "어떤 θ가 hypothesis를 가장 강하게 만드는지, 잘 표현하는지"를 푸는 것이다.
압정의 결과는 θ를 따르기때문에 이 θ를 잘 골라야 우리의 hypothesis를 강하게 만들 수 있다.
θ의 후보 중에 우리가 생각한 확률을 최대화하는 θ를 hat{θ} 로 표현한다.

우리가 앞서 이야기해온 식들을 적용해보면,
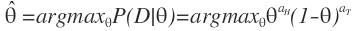
로 표현할 수 있고, log function을 사용해서 아래와 같이 나타낼 수 있다.

* 왜 log를 사용하는걸까?
MLE는 파라미터 θ에서 likelihood가 Maximum일 때 나오는 데이터를 계산하는 것이다.
Maximize문제를 풀 때 미분을 쓰면 극점을 쉽게 찾을 수 있고
미분 계산을 간단하게 만들기 위해 log trick을 많이 쓴다.
값에 log를 취하게 되면 미분이 간편해지기 때문에 log를 쓰는 것.
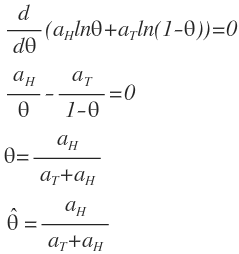
θ에 대해 미분하면 위와 같이 나온다.
다시 압정 게임으로 돌아와보면
5번 던졌을 때 Head가 3번 나온 시도를 Binomial distribution으로 가정하여 MLE의 관점에서 계산해보면
θ는 3/5 = 0.6이다.
그러니까 Head를 선택하는게 게임에서 이길 확률이 높다.
이전에 "5번 던져봤는데 3번 head나왔으니까 head일 확률이 높아"라고 하는 것 보다 훨씬 강한 근거가 생겼다.
다시 질문..
더 많이 던져보면 어떨까? 50번 던지는게 더 좋지않을까?
맞다. 더 여러번 해보는 것이 좋다.
왜 그럴까?
우리가 구한 것은 θ의 추정치인 hat{θ}이다.
true value θ가 아니라 error가 섞여있다는 것이다.

추정한 hat{θ} - true θ가 error ε보다 크거나 같을 확률P는 우변보다 작거나 같다.
ε가 커지면 우변은 작아지게 된다.
시도한 횟수인 N이 커지게되면 그만큼 확률P는 작아지게 된다.
따라서, 시도가 많아질 수록 더욱 정확해진다는 의미가 된다.
예) 동전을 두번 던져서 (앞,앞)이 나왔다.
동전을 스무번 던져서 (앞 7번, 뒤 13번)이 나왔다.
동전을 200번 던져서 (앞 108번, 뒤 92번)이 나왔다.
점점 시도가 많아질수록 estimation값은 true value에 가까워지게 된다.(오차가 적어진다는 의미)
이렇게 시도가 많아질 수록 정확해짐을 알 수 있었는데 이 식을 사용해서
0.01%경우에서 ε = 0.1를 얻으려면 몇 번 시도해봐야하는지도 알 수 있을 것이다.
이러한 것을 지칭하는 말이 있다.
"Probably Approximate Correct한 learning"
PAC leaning이라고 한다.
Probably, 0.01% 경우에서 Approximately, ε = 0.1 내에서 correct한 결과값이 아마 hat{θ}이지 않을까?라고 하는 것이다.
2019/04/30 - [Study] - (edwith) 인공지능 및 기계학습 개론 (1) - 문일철 교수님
(edwith) 인공지능 및 기계학습 개론 (1) - 문일철 교수님
edwith에서 제공하는 인공지능 및 기계학습 개론 - 문일철 | KOOC (KAIST Open Online Course) 를 수강하며 정리한 글입니다. Motivation Machine learning, AI, Datamining 등 빅데이터를 활용한 기술들이 현 시..
whereisend.tistory.com
'Machine Learning' 카테고리의 다른 글
| 코세라 - 01 Model Representation (0) | 2019.08.30 |
|---|---|
| 코세라 - 00 Machine Learning (0) | 2019.08.30 |
| (edwith) 인공지능 및 기계학습 개론 (1) Machine Learning - 문일철 교수님 (0) | 2019.04.30 |
| 구글 머신러닝 스터디잼 중급반 후기 + 반성(?) (0) | 2019.04.15 |
| tensorflow / tensorflow-gpu 설치, GPU 사용하는 방법 (0) | 2019.04.03 |